선형 회귀분석 (Linear Regression)
이번 포스팅은 머신러닝의 근간이 되는 친구인 Regression 에 대해서 간단하게 알아보자.
사실 간단하게 내용을 정리할 수가 없다. 위대한 학자 Gauss가 어떻게 Least square라는 방법을 발견했으며, 회귀분석은 왜 회귀분석이며 그래서 이게 뭐 어떤걸 나타내며, 어떤 가정하에서는 다른 Regression method를 사용해야하며 등등 내로라하는 기관의 전공 대학원 학자들도 완벽하게 숙지하지 못한 사람이 꽤 있다.
그래서, 이 포스팅에선 차, 포 다 떼고
- 이놈이 무엇인지!
- 뭐 왜 필요한지!
- 머신러닝때 어떻게 쓰이는건지!
에 집중해서 약간의 수학(?)처럼 보이는 수식으로 설명을 한 뒤, 바로 예제 코드로 넘어가서 “이렇게 쓰여요~” 라는 것을 알아보겠다.
우선 지도학습이 어떤 개념인지 알고 있다는 가정하에… 아래의 그림을 보자.
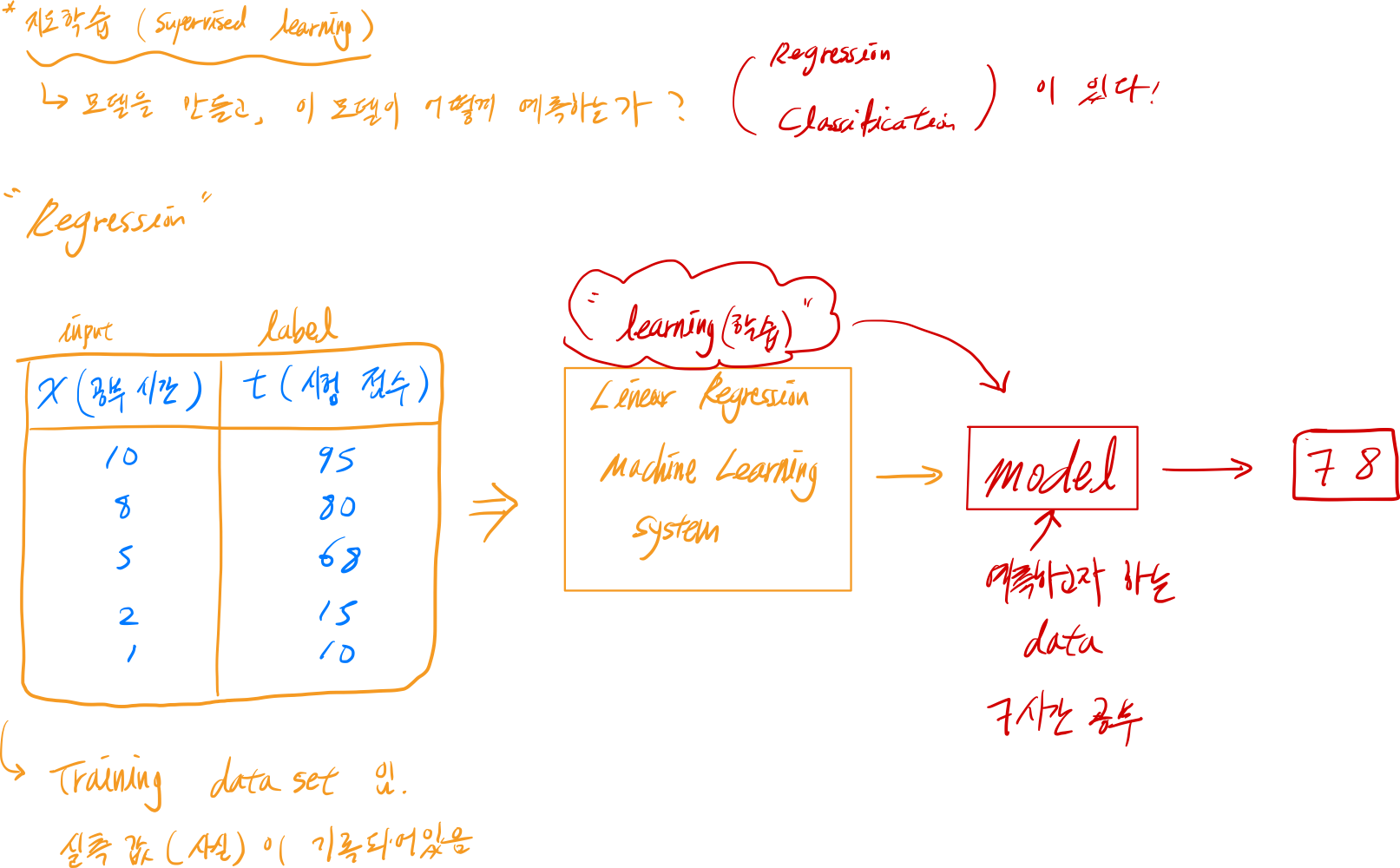
그림 중간에 보이는 테이블을 보자.
공부 시간이 x에 저장되어 독립변수로 작용하고, 시험점수는 t라는 target (aka label)이 되어 독립변수의 값에 의해 변하는 종속변수이다.
이런 일련의 관측된 값이 어떤 데이터 셋 안에 저장이 되어있을 때, 우리는 기계를 학습시킬 수 있다. 그 학습을 통해 김아무개씨가 7시간을 공부했을 때 시험에서 몇점을 받을 수 있는지 예측할 수 있게 된다.
이렇게 예측을 하려면 “옛다 임의의 점수 몇점이다~” 이렇게 줄 수는 없는 노릇이다.
논리적인 근거에 기초해서 어떻게, 왜 몇점이 나왔는지 알수 있어야한다.
이런 로직을 담당해주는 부분이 Regression이다.
이 regression은 어떤 가정하에서 쓰이게 된다면 일반화 시킬 수 있는 인과관계를 규명할 수 있는 강력한 수단이다. (물론 무분별한 사용은 무의미한 결과만 도출할 뿐이다.)
자 그럼 어떻게 사용하는지 바로 알아보자.
Classic Linear Regression 이라는 아주 고전적이며 자주 쓰이는 이 회귀분석 수식의 기본적인 생김새는
\[\hat{y} = \beta_0 + \sum_{i=1}^{p}\beta_i x_i\]이렇게 생겼다. 어째 자세히 보면 어딘가 익숙한 거 같다.. $ y = ax + b $ ! 이 단순 기울기와 절편이 있는 직선 그래프 함수와 비슷하게 생기지 않았는가?
그래서 이 친구도 직선의 속성을 갖고 있어서 선형 회귀분석이라고 불린다.
Machine Learning에서는 이 직선을 표현할 때 조금 다르게 표현을 하는데
\[y = Wx + b\]라고 표현을 한다. $ W $ 는 weight의 의미를 가진 가중치이며, $ b $는 bias라고 불린다.
이게 정말 중요하고 유의미해질 때가 있는데, 바로 실측 데이터 target t과 회귀분석으로 추정된 데이터 $\hat{y}$ 의 차이를 비교했을 때이다.
왜냐고? 차이의 값을 오차(error)라고 표현을 하는데, 차이의 값이 크다면 해당 직선이 데이터를 잘 표현하고 있지 못하단 소리니깐!
그래서 우리가 ML을 사용하는 대부분의 경우는 error의 값이 최소화가 되는 $ W $ 와 $ b $ 를 찾기 위함이다.
또한 error의 값을 제곱하여 합산한 형태를 우리는 쓰게 될 것이다. (왜 이런지 궁금하면 계량경제학의 회귀이론이나 통계학을 참고하기 바란다.. 너무 복잡한 설명이 될 거 같아서 이 포스팅에선 생략한다.)
이 error함수를 ML에선 손실 함수 (loss function)라고 표현을 한다.
수식을 이용하여 표현을 해보자면:
\[E(W,b) = \frac{(t_1 - y_1)^2 + (t_2 - y_2)^2 + . . . + (t_n - y_n)^2}{n}\] \[E(W, b) = \frac{[t_1 - (Wx_1 + b)]^2 + [t_2 - (Wx_2 + b)]^2 + . . . + [t_n - (Wx_n + b)]^2} {n}\]따러서, $ E(W, b) = \frac{1}{n} \sum_{i=1}^{n}[t_i - (Wx_i + b)]^2 의 형태로 나타낼 수 있다.
이 loss function은 $ W $ 와 $ b $ 의 함수이다. 왜냐고? 입력값인 $ x_i $와 레이블인 $ t_i $는 이미 정해져있기 때문이다.
또한, 식 전체에 적용된 제곱을 보면 2차 함수이며, U-모양의 컨벡스(Convex)형태를 띄고 있는 것을 알아볼 수 있을것이다.
따라서 ML에서 이 손실함수의 쓰임새는 손실함수의 값을 최소로 만들어주는 $ W $ 와 $ b $를 구하는 모델을 만드는 것이다.
경사하강법 (gradient descent)
최적의 가중치와 바이어스 값을 찾아가는 알고리즘으로 쓰이는 경사하강법을 간략하게 설명하자면
- 임의의 가중치 $W$ 를 선택
- 손실함수 곡선 어느 위치에서든 직선의 기울기를 구한다 (다시 말하면 해당점의 미분 계수를 찾는다. 아래의 그래프를 보자.).
- $ W’ = W - \alpha \times \frac{\partial E(W,b)}{\partial W} $, where $ \alpha $는 learning rate라는 상수
- learning rate는 곡선의 한점에서 다른 점으로 이동할 때, 값이 너무 크게 올라가는것을 방지하기 위한 수단으로 쓰인다.
- learning rate는 사용자가 임의로 customizing 해야한다. (보통은 작은 수로 설정 e.g. 0.001)
- 반복횟수를 지정해줘야한다.
- 이것 또한 임의로 몇번 반복해야하는지 정해줘야함.
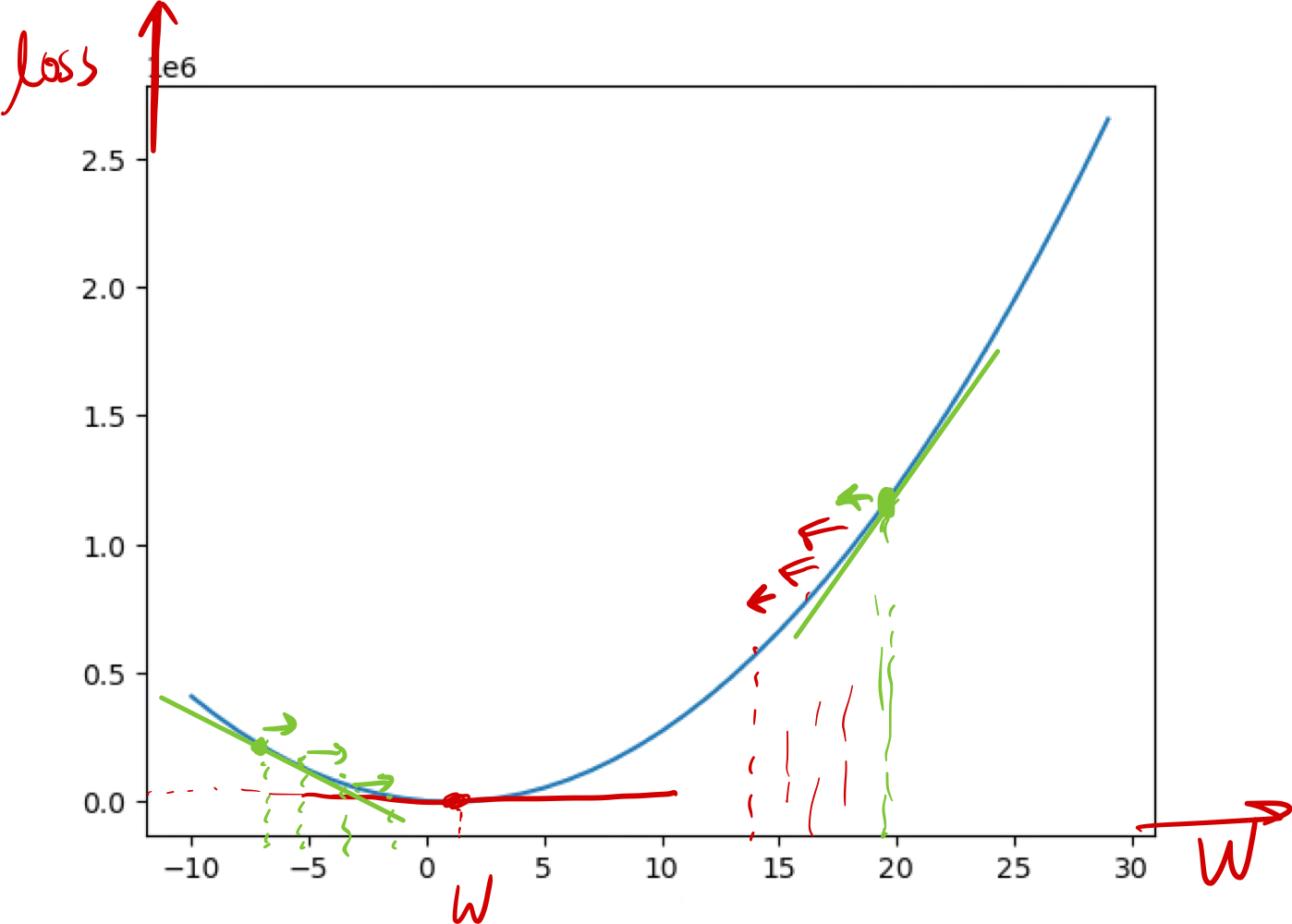
자 그러면 지금까지의 작업을 흐름에 따라 한 번 살펴보자 (밑에 손으로 그린 flow chart를 보자)

실측 데이터를 통해 모델을 만들고, 경사하강법으로 손실함수의 최소 값을 알려주는 $W$와 $b$를 찾아낸다.
실전 파이썬 코드
이제 실전에 선형 회귀 분석을 이용해보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
import numpy as np # 이번 예제에선 numpy만 사용할 것임
# 1. training data set 준비
x_data = np.arange([1, 2, 3, 4, 5]).reshape(5, 1) # 5x1 행렬로 x(input) 값을 설정
t_data = np.arange([3, 5, 7, 9, 11]).reshape(5, 1) # 5x1 행렬로 t(레이블) 값을 설정
# 2. 모델 정의 (가중치 W 와 바이아스 b값을 난수로 주자)
W = np.random.rand(1, 1) # 1x1 행렬로 [0,1) 사이의 값을 설정
b = np.random.rand(1) # 1차원 벡터로 [0, 1) 사이의 값을 설정
# 3. loss function
def loss_function(input_value):
"""
input value는 W와 b값을 포함하고 있다
"""
W = input_value[0].reshape(1, 1) # 원래 1x1 행렬이지만 그래도 다시 설정을 해주었음
b = input_value[1]
# model y = Wx + b
y = np.dot(x_data, W) + b # b는 브로드캐스팅 됨
# x_data x W => 5x1 행렬
# (5x1) (1x1) = (5x1)
return np.mean(np.power(t_data - y, 2)) # (실측치 - 예측치)의 제곱값의 평균
# 4. 미분을 수행할 함수
def numerical_derivative(f, x):
"""
편미분을 여러번 돌려야함 (vector of partial derivatives)
f: loss function에 대해서 돌림
"""
delta_x = 1e-4 # x 변화량의 크기 (극한 대신 아주 작은 수로 대체)
derivative_x = np.zeros_like(x) # x와 똑같은 shape을 가진 배열(혹은 행렬) 생성 (요소값은 0임)
it = np.nditer(x, flags=['multi_index']) # iterator 하나 생성. 플래그는 멀티 인덱스 설정
while not it.finished:
idx = it.multi_index
tmp = x[idx] # 임시 변수로 x[idx] 의 원값을 저장
x[idx] = tmp + delta_x # 전향 차분
fx_plus_delta_x = f(x) # 첫번째 인자로 들어온 함수를 대입
x[idx] = tmp - delta_x # 후향 차분
fx_minus_delta_x = f(x) # 첫번째 인자로 들어온 함수를 다시 대입
# 중앙 차분
derivative_x[idx] = (fx_plus_delta_x - fx_minus_delta_x) / (2 * delta_x)
x[idx] = tmp # x값 원상태로 복구
it.iternext() # 다음 인덱스로 넘어가자
return derivative_x
# 5. Learning rate 설정
learning_rate = 1e-4 # 커스터마이징한 값임.
# 6. 반복 학습을 진행
for step in range(100000):
# 최적의 loss값인가요? => 이거 판단하는게 쉽지 않음. 딱 0으로 떨어져서 끝나면 얼마나 좋겠어..
# 넘겨줄 파라미터부터 구하자 => ravel() 이용하자. 뭐든지 1차원으로 바꿈
input_param = np.concatenate((W.ravel(), b.ravel()), axis=0) # 열방향 => [W, b] 이렇게 들어가게 됨
tmp = learning_rate * numerical_derivative(loss_func, input_param) # [W의 편미분 값, b의 편미분 값]
W = W - tmp[0].reshape(1, 1) # 얘도 broadcasting 되긴 하는데 reshape 잡자.
b = b - tmp[1] # broadcasting
if step % 10000 == 0: # 10만번의 학습이 진행되는 동안, 중간 과정 10번 체크
print('W의 값은 {}, b의 값은 {}'.format(W, b))
나같은 경우엔 이렇게 실행을 시키면…
1
2
3
4
5
6
7
8
9
10
11
12
13
W의 값은 [[0.68000733]], b의 값은 [0.97612513]
W의 값은 [[1.93730769]], b의 값은 [1.22633913]
W의 값은 [[1.9552927]], b의 값은 [1.16140755]
W의 값은 [[1.96811821]], b의 값은 [1.11510337]
W의 값은 [[1.97726438]], b의 값은 [1.08208281]
W의 값은 [[1.98378671]], b의 값은 [1.05853511]
W의 값은 [[1.98843794]], b의 값은 [1.04174271]
W의 값은 [[1.99175483]], b의 값은 [1.02976767]
W의 값은 [[1.99412018]], b의 값은 [1.021228]
W의 값은 [[1.99580697]], b의 값은 [1.01513817]
이렇게 값이 나왔다!
물론 seed를 잡고 실행하면 난수에 관해서 고정된 값이 출력이 되기에, 더 편할 수도 있다. 참고하자.
자 그럼 $ W $와 $b$의 값을 갖고 뭘 해야하겠는가??
y = Wx + b를 예측하기 딱 좋지 않는가?
임의의 값 x를 설정하자. 음… 7이란 값을 주겠다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
predict_value = np.array([[7]])
H = np.dot(predict_value, W) + b # hypothesis model X = predict_value
print(H)
"""
결과값: [[14.98986402]]
X가 공부시간이고, y가 시험 성적이라고 가정을 해본다면
"7시간 공부했을때 약 15점에 가까운 성적을 받을 수 있으리라 예측된다." 라고 해석할 수 있겠다.
물론 이 값은
x_data = np.arange([1, 2, 3, 4, 5]).reshape(5, 1) # 5x1 행렬로 x(input) 값을 설정
t_data = np.arange([3, 5, 7, 9, 11]).reshape(5, 1) # 5x1 행렬로 t(레이블) 값을 설정
이 training data set에 의거한 결과임을 잊지 말자.
"""
이렇게 어떻게 Linear Regression기법이 머신러닝에서 사용되는지 경사하강법을 통해 알아보았다.
그럼 안녕 👋