Logistic Regression
지난번 포스팅에선 Machine Learning 으로 어떻게 회귀분석을 하는지 알아보았다.
오늘은 레이블(t) 값이 0과 1 둘중 하나인 이산(discrete) 형태를 띄고 있을 때 어떻게 회귀분석을 할 수 있는지 알아보자.
사실 학계에서는 이런 이산변수를 다루는 일보다 연속적인 값의 형태를 가진 종속변수를 다양한 방법론을 통해 분석하는 경우가 많다.
( e.g. 총 노동 시간의 변화, 범죄율 증가 및 감소에 대한 연구, 정책에 따른 출산율 변화 등 )
하지만 머신러닝에선 연속적인 값을 종속변수로 취하는 경우보다 0 또는 1, True/False, 합격/불합격 등과 같이 이진 변수 (binary variable)를 상대적으로 많이 사용할 일이 잦다.
(e.g. Email span 판별, 금융 상품 가격이 오를까 내릴까, MRI등 의료용 사진을 이용한 병 진단 여부, 신용카드 사용시 도난카드 판별, 불량품인지 아닌지 등)
이럴때 사용하는 모델을 Classification Model이라고 부르며 Logistic Regression이라는 회귀분석을 사용한다.
Logistic Regression의 개념도
간단하게 밑에 플로우 차트를 통해 Logistic Regression의 개념도를 살펴보자.

가볍게 살펴보니깐, “오? Linear Regression과 비슷한데 뭐가 더 추가된거네?”라고 생각하면 좋을거 같다.
실제로 중간에 활성화 함수 (activation function)라는 것이 하나가 추가가 되어 Linear Regression의 결과값을 0과 1사이의 확률로 나타내고,
또 임계 함수 (Threshold function)이 추가되어 0/1, 맞다/틀리다 등과 같은 이진 변수로 결괏값을 나타내어준다.
Sigmoid

Logistic Regression을 사용한다면 sigmoid와 친해질 필요가 있다. 수식을 이해하고, loss function을 이해하는 정도라면 충분하다고 생각한다.
| 선형 회귀 | 로지스틱 회귀 | |
|---|---|---|
| 기본 수식 | $ y = WX + b $ | $ y = \frac{1}{1+e^{-(WX+b)}} $ |
| Loss function | $ E(w,b) = \frac{1}{n}\sum^{n}_{i=1}[t_i - (w_ix_i+b)]^2 $ | |
| $ E(w,b) = -\sum^{n}_{i=1}[t_ilog(y_i)+(1-t_i)log(1-y_i)] $ |
최적의 $ W $ 와 $b$를 구하기 위해 손실함수를 미분하여 $W$, $b$를 갱신한다는 점에서 선형회귀와 비슷하다고 볼 수 있다. 하지만 문제는 로지스틱 회귀 분석의 경우 손실함수의 그래프 곡선이 convexity의 성격을 갖고 있지 않아서 실제로 loss function의 값이 최소화 되었는지 모른다는 점이다.
이를 방지하기 위해 손실함수에 log function이 씌워지는데, 이를 머신러닝에선 “Cross Entropy” 또는 “log loss“라고 부른다.
밑의 그림은 Cross Entropy를 이용하여 loss 값을 최소화 시키는 프로세스를 플로우 차트로 표현을 해보았다. (참고만 하자)
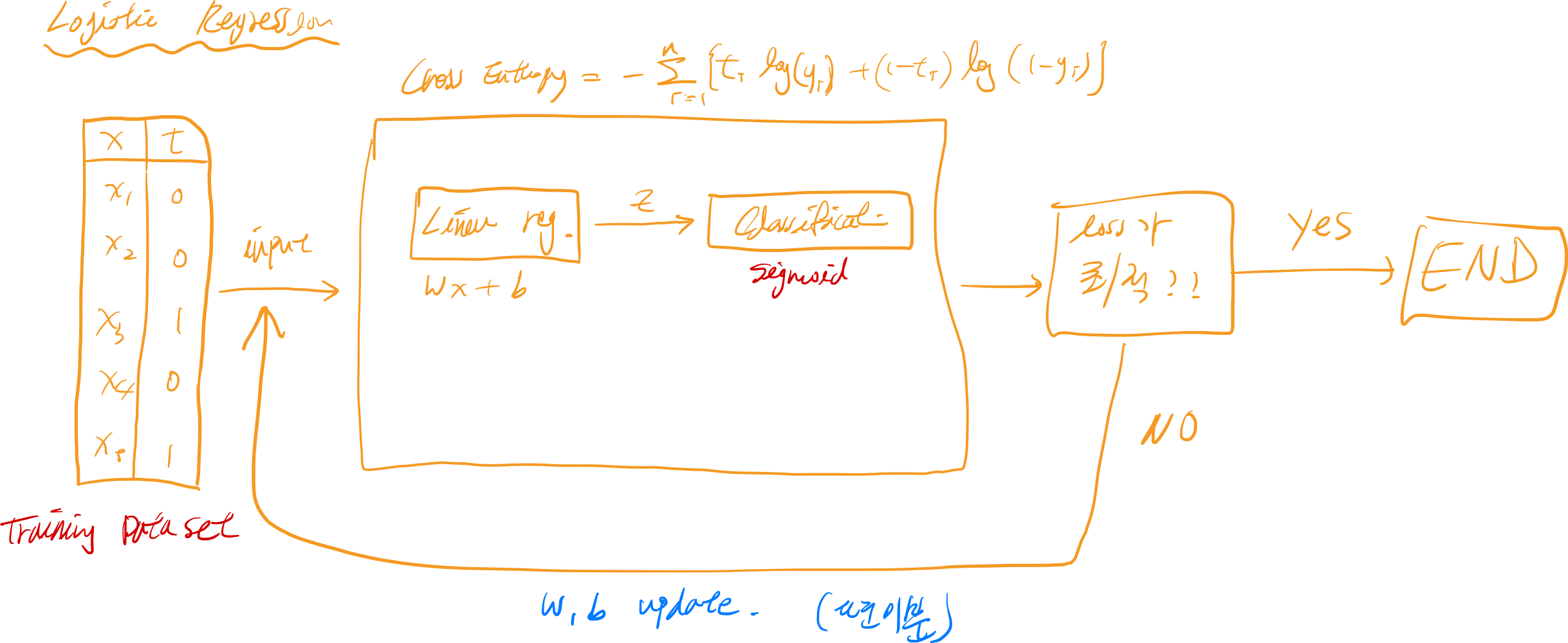
다음 포스팅에선 sklearn, python 그리고 tesorflow를 통해 직접 logistic regression을 구현해보도록 하자!
오늘은 끄읏. 👋