분류 성능 평가 지표 (metric)
일반 선형 회귀분석과 다르게 Logistic Regression 으로 넘어온다면, 내가 만든 모델이 잘되는지 성능을 평가하는 지표가 있다. 그걸 분류 성능 평가 지표 (metric)이라고 부른다.
Q. 왜 logistic만 있나요? 연속형 실수 값을 갖는 레이블을 분석하는 Regression의 경우 연속형 실수의 값을 맞추기는 불가능하기때문이다. 반면, 이진 분류는 맞다/틀리다 둘 중하나로 나뉘기때문에 머신러닝의 효능을 평가할 수 있는 방법이 있다.
여러가지의 평가지표가 있으며, 대표적인 세가지를 소개해보자면:
- Precision (정밀도): 모델이 true라고 분류한 것중 실제 true인것을 맞춘 비율
- Recall (재현율): 실제 true인 것중에 모델이 true로 예측한 비율
- Accuracy (정확도): 모델이 예측한 것이 맞춘 비율
벌써부터 헷갈리지 않는가? 하지만 이 평가 지표가 여러개인데에는 다 이유가 있다.
지금부터 천천히 알아보자
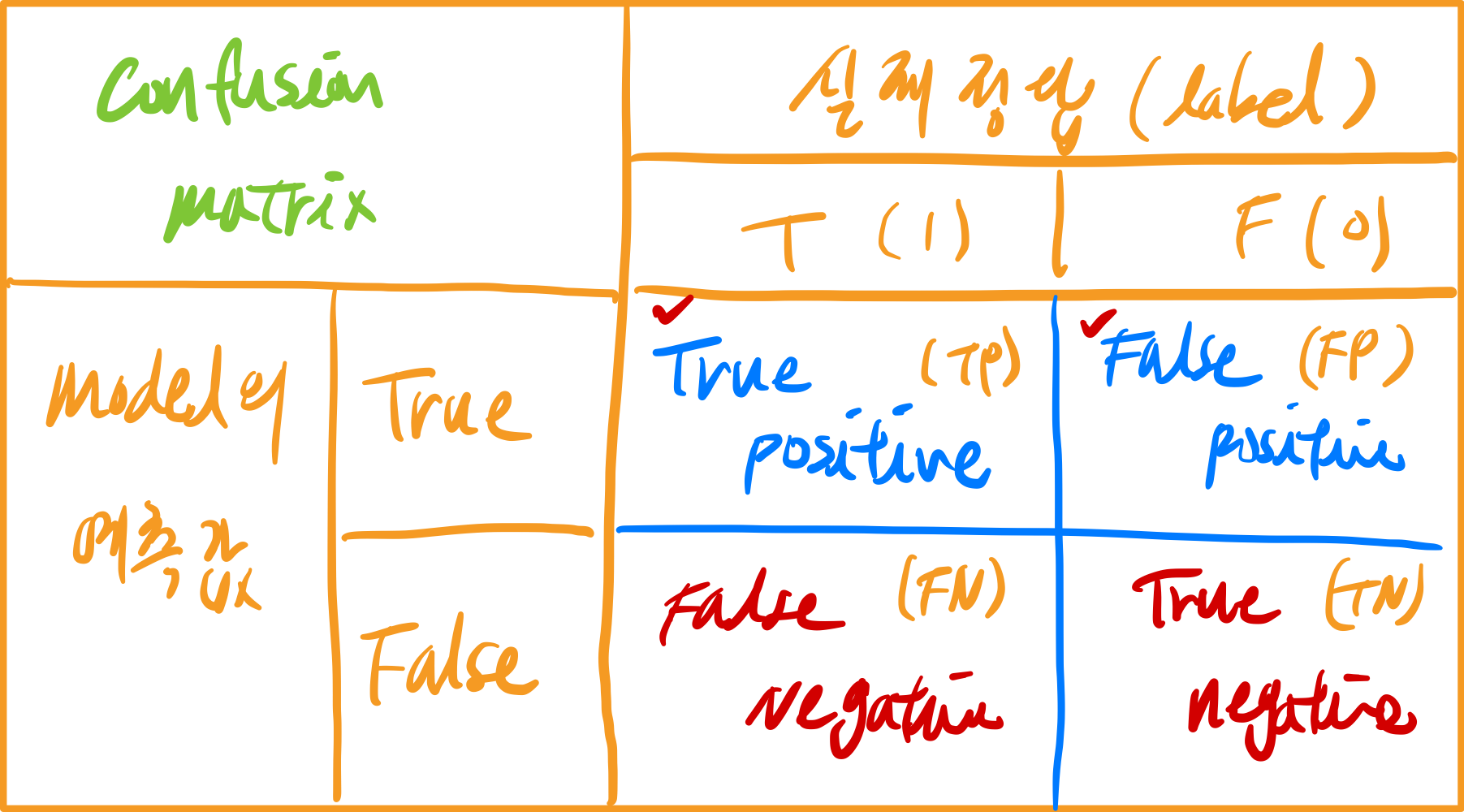
위 테이블은 confusion matrix라고 불리는 평가 지표에 쓰이는 요소를 담고 있는 테이블이다.
confusion이라는 단어 그대로 헷갈리니 이해하고 넘어가는 것이 중요하다.
나름대로 특징이 있는데 몇가지 꼽아보자면,
- 모델의 관점에서 테이블을 읽는것이 중요하며, (열방향으로 읽기)
- model이 True라고 예측한 행의 값들을 보면 뒷 단어가 positive인것을 알 수 있다.
- model이 Negative라고 예측한 행의 값들을 보면 뒷 단어가 negative인것을 알 수 있다.
- 실측 데이터의 관점에서 테이블을 읽는것이 중요하다 (행방향으로 읽기)
- model의 예측값이 실측 데이터와 일치한다면 True라고 표기되는 것을 알 수 있다
- model의 예측값이 실측 데이터와 다르다면 False라고 표기되는 것을 알 수 있다
실제 ML에서는 앞글자를 따서 TP, FP, TN, FN 으로 표기한다는 것을 알아두자.
자 그럼 맨 처음 언급했던 precision, recall 그리고 accuracy를 confusion matrix요소로 표현을 하면 어떻게 될까?
precision (정밀도):
$ precision = \frac{TP}{TP+FP} $
recall (재현율) – aka ‘hit rate’, ‘sensitivity’:
$ recall = \frac{TP}{TP+FN} $
Accuracy(정확도):
$ accuracy = \frac{TP + TN}{TP + FP + FN + TN} $
정확도가 가장 직관적이지 않는가? 내가 맞다 틀리다 예측한 것중에 맞은 개수에 대한 비율.
그런데 정확도는 큰 단점이 있다. 바로 불균형한 레이블 값 분포에서 머신러닝 성능을 평가한다면 적합한 평가 지표로 활용이 되지 않는다.
좀 더 직관적으로 얘기해보자. 예를 들어 100개의 데이터가 있는데, 0의 값을 갖는 레이블이 97개 1의 값을 갖는 레이블이 3개라고 가정해보자.
(e.g. 제조 공장내 불량품, 암 CT 결과 등이 한쪽으로 치우쳐진 레이블 값을 갖고 있음.)
이런 경우 무조건 0으로 예측을 한다하더라도 정확도는 97%가 된다.
이런 이전 (binary) 분류의 성향을 갖는 경우 domain의 bias에 상당히 민감하다.
5:5 비율일 때 효과가 정말 좋은 지표임을 기억하라.
recall 과 precision을 면밀히 살펴보면 둘은 “반비례” 관계에 있음을 알 수 있다.
precision을 높이면 recall이 떨어지고,
recall을 높이자니, precision이 떨어진다 (툭 까놓고 recall은 그냥 모델이 positive만 주구장창 예측하면 높아진다. 근데 그러면 FP요소를 갖고 있는 precision이 떨어진다.)
위와 같은 복잡한 수식과 더불어 반대로 움직이는 이런 trade-off 관계가 metric을 이해하는데 장애가 되어 나타나곤 한다.
이러한 평가 지표 외에도 F1 score, Fall-out 등이 있는데 이건 나중에 다뤄보도록 하자.
👋