Linear Regression Data Handling
이번 포스팅은 파이썬과 경사하강법 (Gradient Descent Algorithm)을 이용하여 지난번보다 더 정확한 회귀분석을 해보려고 한다. 그리고 최종적으로 내가 짠 코드와 알고리즘이 scikit learn 패키지에서 제공한 linear_model에 모듈에 비해서 얼마나 정확한지 비교해보려고 한다.
“굳이 좋은 라이브러리 놔두고 왜 파이썬으로, 로우레벨 스타일로 직접 코딩을 해야하느냐?” 라고 의문을 가질 수도 있다.
첫째로, 직접 A to Z 동작원리를 파악하고 구조를 파악하여 사용한다면 라이브러리에 대한 깊은 이해도를 갖고 잘활용할 수 있으리라 생각하기 때문이며
둘째로, 어떤 유형의 자료구조나 복잡한 상황 등에 따라서sklearn사용에 한계가 있을 수 있기 때문이다.
마지막으로, (이게 제일 중요함) 결국 TensorFlow로 구현할 때, GradientDescentOptimizer()라는 메서드를 사용하게 되는데, 이때 경사하강법 (Gradient Descent Algorithm)을 이해하지 못한채로 사용한다면 무슨 의미가 있겠는가.. 암기식 교육에 지나지 않는다.
우리가 미적분을 할 때, 공식을 외워서 활용하기 이전에, 어떻게 극한으로부터 미분값이 도출되는지 증명을 해보며 원리를 이해하는 과정을 겪는다면 훨씬 미분에 대한 활용폭이 넓어지는 것과 비슷한 과정이라 생각한다.
서두가 길었다. 데이터는 ozone.csv 데이터를 사용하였는데 데이터 파일은 깃헙에 남겨두겠다!
환경부터 설정하자.
1
2
3
4
5
6
import numpy as np # ndarray가 기본
import pandas as pd # data 처리 및 loading
import matplotlib.pyplot as plt # scatter 찍고, scikit learn이 구현한게 비슷한지 확인용
from sklearn import linear_model
from scipy import stats # z score값을 이용한 정규화 (normalisation) 작업에 사용
from sklearn.preprocessing import MinMaxScaler # min max scaling 사용을 할건데 이것 또한 sklearn의 도움을 받을것임.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 수치미분 함수. 없다면 복사해서 사용하길 바람
def numerical_derivative(f, x):
"""
편미분을 여러번 돌려야함 (vector of partial derivatives)
f: loss function에 대해서 돌림
x: loss function에서 사용될 1차원 이상의 배열 데이터
"""
delta_x = 1e-4 # x 변화량의 크기 (극한 대신 아주 작은 수로 대체)
derivative_x = np.zeros_like(x) # x와 똑같은 shape이며 요소를 0으로 갖고 있는 배열(or 행렬) 생성
it = np.nditer(x, flags=['multi_index']) # iterator 하나 생성. 플래그는 멀티 인덱스 설정
while not it.finished:
idx = it.multi_index
tmp = x[idx] # 임시 변수로 x[idx] 의 원값을 저장
x[idx] = tmp + delta_x # 전향 차분
fx_plus_delta_x = f(x) # 첫번째 인자로 들어온 함수를 대입
x[idx] = tmp - delta_x # 후향 차분
fx_minus_delta_x = f(x) # 첫번째 인자로 들어온 함수를 다시 대입
# 중앙 차분
derivative_x[idx] = (fx_plus_delta_x - fx_minus_delta_x) / (2 * delta_x)
x[idx] = tmp # x값 원상태로 복구
it.iternext() # 다음 인덱스로 넘어가자
return derivative_x
데이터 로딩
1
2
3
4
5
6
# Raw Data Loading
df = pd.read_csv('./data/ozone/ozone.csv', sep=',') # 경로는 본인의 환경에 맞춰 사용하자.
display(df.head()) # 데이터 한번 찍어주고.
training_data_set = df[['Temp', 'Ozone']] # 우선 단순 선형 회귀, 독립변수를 하나만 갖자. (temp)
1. 결치값 처리
NaN 데이터를 처리하는 방법은 여러가지가 있다.
- 값을 대체 (대체시 임의의 숫자가 아닌 논리에 의거해서 값을 결정)
- 값을 삭제
경우에 따라 이상적인 방안이 있기는 하나, 이번 포스팅에선 값을 삭제하고 가자.
1
2
training_data = training_data_set.dropna(how='any') # .dropna 메소드를 사용
display(training_data.shape) # (116, 2)
2. 이상치(outliers) 처리
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 이상치 처리
# 온도에 대해서도 이상한 값이 있는지 판단후 처리 (지대점 처리)
# 오존값에서도 이상한 값이 있으면 판단후 처리 (outlier)
# 아웃라이어 처리시 항상 조심해야함.
# 온도에 대한 이상치를 날리고, 이후에 오존에 대해 날린다고 하자.
# 근데 첫 이상치를 떼어내면, 하나가 떼어진 상태에서 다시 이상치를 확인하면 아웃라이어가 바뀔수 있음.
# 남은 데이터로 처리를 하면 기준 자체가 바뀐다.
# Temp에 대한 이상치(지대점) 처리
zscore_threshold = 1.8 # zscore 값을 잡았다. 보통 1.96일때 약 97%의 데이터를 포함한다.
# 여기선 1.8로 조금은 느슨하게 잡았다
# 온도에 있는 지대값을 추출
np.abs(stats.zscore(training_data['Temp'])) # 절대값으로 변환. zscore threshold랑 비교해야함
np.abs(stats.zscore(training_data['Temp'])) > zscore_threshold # boolean mask 가 나옴
# False로 나오면 지대값이 아니란 소리. True라면 아웃라이어, 지대값, 이상치란 소리. (z score를 기준으로 했을때)
outlier = training_data['Temp'][ np.abs(stats.zscore(training_data['Temp'])) > zscore_threshold ] # True 부분만 뽑아냄.
print(outlier) # 지대점
# training_data['Temp'].isin(outlier) # False의 의미가 지대점이 아니란 소리임.
~training_data['Temp'].isin(outlier) # 앞에 tilde를 주면서 논리값이 반대로 바뀜.
training_data['Temp'][ ~training_data['Temp'].isin(outlier) ] # 110개의 데이터만 남음
training_data = training_data.loc[ ~training_data['Temp'].isin(outlier), :] # 110 x 2
이번엔 t(레이블)의 값을 갖고 있는 ‘Ozone‘에 대해서 이상치를 처리해보자.
1
2
3
4
# 마찬가지로 outlier 설정
outlier = training_data['Ozone'][ np.abs(stats.zscore(training_data['Ozone'])) > zscore_threshold ]
training_data = training_data.loc[ ~training_data['Ozone'].isin(outlier), :] # 103 rows × 2 columns
여기까지 완료했다면 103개의 case와 2개의 열을 가진 DataFrame으로 정제된다.
3. 정규화 (Normalization)
zscore를 통한 정규화, min-max scaling 등 여러 방법이 있지만 이거에 대한 첨언 및 부연설명은 다른 포스팅에서 알아보도록 하자.
여기서는 Min-Max Normalization을 사용한다.
맨처음 환경을 세팅할 때 불러왔던 sklearn패키지의 preprocessing모듈의 MinMaxScaler 클래스를 이용한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 입력값에 대한 스케일링을 하는 객체를 만들것임
scaler_x = MinMaxScaler() # scaling 작업을 수행하는 객체를 하나 생성 (입력값 처리 하는놈 1개, label 처리 하는 놈 1개)
scaler_y = MinMaxScaler()
scaler_x.fit(training_data['Temp'].values.reshape(-1,1))
scaler_y.fit(training_data['Ozone'].values.reshape(-1,1))
# fitting 작업을 함. 변환시키는 작업은 아님.
# 최소, 최댓값을 알기위한 작업.
# fit안에는 2차원 ndarray로만 나와야함
# data의 개수, 최대, 최소값들을 scaler에 저장!
# 밑에는 df안에 있는 독립변수와 종속변수의 스케일을 정규화하는 코드임.
training_data['Temp'] = scaler_x.transform(training_data['Temp'].values.reshape(-1,1))
training_data['Ozone'] = scaler_y.transform(training_data['Ozone'].values.reshape(-1,1))
( “transform을 하는데 왜 reshape을 하는가?” 의문이 든다면, 선형대수학에서 매트릭스 트랜스포즈 할 때 행렬 형태에서만 가능하다고 치부하면 이해하기가 쉽다.)
이제 training data set에 대한 준비가 끝났다. 머신러닝 돌릴일만 남았단 소리다. 😉
4. Training Data Set
1
2
x_data = training_data['Temp'].values.reshape(-1, 1)
t_data = training_data['Ozone'].values.reshape(-1, 1)
5. W와 b 설정 (W: weight (가중치) & b: bias (편향))
W와 b는 난수로 잡아둔다.
단, W같은 경우는 독립변수와 매트릭스 곱하기 연산이 필요하기 때문에, “1x1” 행렬로 변환시켜서 난수를 받는다.
1
2
3
# W와 b 를 정의 (Weight & bias)
W = np.random.rand(1,1) # 1x1 (2차원)
b = np.random.rand(1) # 1차원 백터
6. 예측 함수와 손실 함수 정의, 그리고 Learning rate 설정
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 우리가 만든 파이썬으로 구현한 예측함수 하나 정의
def predict(x):
return np.dot(x, W) + b
# W와 b를 구하려면? loss function이 필요하다. 또 수치미분 함수가 필요하다.
def loss_func(input_obj): # input_obj는 [W의 값, b의 값] 1차원 ndarray로 받음
input_W = input_obj[0].reshape(1, 1) # 2차원 매트릭스
input_b = input_obj[1]
# 평균제곱오차를 구해야함 => loss 함수의 값. 예측치를 알아야함!
y = np.dot(x_data, input_W) + input_b # 입력값에 대해 현재 W와 b를 이용하여 예측치 계산
return np.mean(np.power((t_data - y), 2)) # [실제 값(t) - 예측값(y)] 의 제곱.
# learning rate 상수 설정
learning_rate = 1e-4
위 코드를 읽다보면 “엥 수치미분 함수는 어디갔지?” 의문이 들수도 있는데, 초기 라이브러리 불러오면서 세팅할때 같이 빼두었다.
7. 반복학습 고고 ⚙️
1
2
3
4
5
6
7
8
9
10
11
12
13
# 이제 준비된 내용을 갖고 반복학습을 진행하자!
for step in range(300000):
input_param = np.concatenate((W.ravel(), b.ravel()), axis=0) # W와 b를 1차원으로 만들어서 연결시킨다.
result_derivative = learning_rate * numerical_derivative(loss_func, input_param)
W = W - result_derivative[0].reshape(-1, 1)
b = b - result_derivative[1]
if step % 30000 == 0:
print('loss: {}'.format(loss_func(input_param))) # loss 값이 작아야 좋은것임. 0에 가까워야 훌륭스.
# loss값이 크다면, learning rate 수정과 반복횟수 증가 등을 통해 재조정을 해보자.
아래에 결과값은 내가 직접 코드를 돌렸을 때 얻은 loss function의 값이다. 너무 크고 만족스럽지 못하다. 데이터 정제, 반복 횟수, 임의로 설정한 learning rate 등등 여러 요인이 있기때문에 완벽할 수는 없다.
1
2
3
4
5
6
7
8
9
10
loss: 1.014186118583775
loss: 0.039834601720002256
loss: 0.03539345409514608
loss: 0.03302686573813619
loss: 0.03176569847265413
loss: 0.031093615866125395
loss: 0.030735459543517578
loss: 0.030544596173185046
loss: 0.0304428840887258
loss: 0.030388681188991663
8. 예측을 해보자
1
2
3
4
5
6
7
8
# 값은 2차원 행렬로 주어야함.
# 함수는 아까 정의해놓았다.
# Temp 값을 화씨 62도로 줘보자.
# 정규화 했기 때문에 아래 변환과정이 필요하다.
scaled_predict_data = scaler_x.transform([[62]])
scaled_result = scaler_y.inverse_transform(predict(scaled_predict_data))
# 정규화된 값을 넣어 예측 함수를 사용했다면, 다시 정규화 이전 상태의 값으로 돌려서 나타냄. 왜? 읽기 쉬우니깐
print(scaled_result)
결과값:
1
[[2.6140319]]
머신러닝.. 이론뿐만아니고 구현도 이렇게 복잡한 거였니?
위에서도 언급했지만, 패키지를 쓰면 훨씬 더 빠르고, 쉽고, 정확하게 값을 도출해낼 수 있다.
같은 데이터를 사용하여 sklearn을 활용해보고, 파이썬의 예측 값과 비교해보자!
SciKit Learn을 이용한 예측
1
2
3
4
5
6
7
# sklearn 패키지 안에 있는 linear_model 모듈에서 LinearRegression 클래스를 이용
model = linear_model.LinearRegression()
model.fit(x_data, t_data) # 데이터는 아까와 같음. fit을 이용해 훈련을 시키자.
scaled_predict_data = scaler_x.transform([[62]]) # 예측을 위해 화씨 62도를 넘겨주었음
scaled_result = model.predict(scaled_predict_data) # 예측된 값을 다시 정규화 -> 원본 형태로 바꿈
print(scaler_y.inverse_transform(scaled_result))
결과값:
1
[[1.75864872]]
- 파이썬에서 로우레벨 스타일 머신러닝의 결과 값: 2.6140319
sklearn으로 한 regression에서의 결과 값: 1.75864872
차이가 상당히 많이난다. 물론 sklearn 이 훨씬 정확하다.
왜 차이가 난걸까? 앞서도 말했지만, 파이썬을 이용한 로우레벨 스타일 코딩에선 상수값을 정해주고, 반복값을 직접 정해줘야하는 순간이 있다.
여기서 대부분 차이가 난다고 생각을 한다.
마지막으로 어떻게, 그리고 얼마나 차이가 나는지를 눈으로 확인해보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
fig = plt.figure()
fig_python = fig.add_subplot(1, 2, 1) # 1행 2열 그중에서 첫번째 (1)
fig_sklearn = fig.add_subplot(1, 2, 2) # 1행 2열 두번째(2)
fig_python.set_title('Using Python') # 첫번째 그래프 타이틀
fig_sklearn.set_title('Using sklearn') # 두번째 그래프 타이틀
fig_python.scatter(x=x_data, y=t_data)
fig_python.plot(x_data, x_data*W.ravel()+b, color='r') # 첫번째 그래프 산점도에 대한 트렌드 라인
# 마찬가지로 두번재 그래프.
fig_sklearn.scatter(training_data['Temp'].values,
training_data['Ozone'].values)
fig_sklearn.plot(training_data['Temp'].values,
training_data['Temp'].values*model.coef_.ravel() + model.intercept_, color='g')
fig.tight_layout()
plt.show()
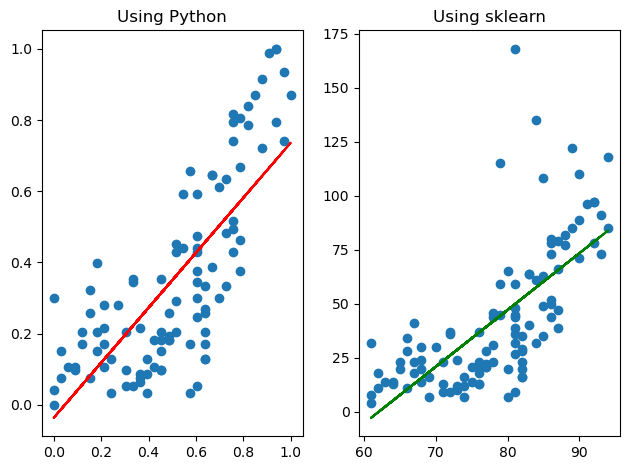
이렇게 추세선에서 차이가 나는것을 볼 수 있다.
아 참고로 산점도 모양이 조금 다른 이유는 python으로 그렸을 때는 정규화를 해놓은 상태였고, 지금은 sklearn에서는 아니다는 점에서 나오는 차이인데.. 이건 필자가 귀찮았기 때문이다. 정규화를 하고 맨위에 있는 outlier를 제외해보았지만 유의미한 변화는 없었다.
오늘은 여기까지…
끄읏트. 👋